environ
vocabularies HIDDEN, CBS, SEQM_3, RELAT_1, XBOOLE_0, PARTFUN1, FUNCT_1, TARSKI, SUBSET_1, ZFMISC_1, RELAT_2, MCART_1, SETFAM_1, FUNCT_2, GROUP_9;
notations HIDDEN, TARSKI, XBOOLE_0, ZFMISC_1, XTUPLE_0, SUBSET_1, SETFAM_1, MCART_1, RELAT_1, RELAT_2, FUNCT_1, RELSET_1, PARTFUN1, FUNCT_2;
definitions TARSKI, XBOOLE_0, PARTFUN1, FUNCT_1, FUNCT_2;
theorems TARSKI, RELAT_1, FUNCT_1, ZFMISC_1, PARTFUN1, GRFUNC_1, RELSET_1, SUBSET_1, XBOOLE_0, XBOOLE_1, RELAT_2, MCART_1, SETFAM_1, XTUPLE_0, FUNCT_2;
schemes FUNCT_1, PARTFUN1, XBOOLE_0, RELSET_1, SUBSET_1, FUNCT_2;
registrations XBOOLE_0, SUBSET_1, RELAT_1, FUNCT_1, PARTFUN1, RELSET_1, GRFUNC_1, ZFMISC_1, FUNCT_2, FUNCOP_1;
constructors HIDDEN, RELAT_2, PARTFUN1, MCART_1, SETFAM_1, RELSET_1, XTUPLE_0, FUNCT_2;
requirements HIDDEN, SUBSET, BOOLE;
equalities PARTFUN1, SUBSET_1;
expansions TARSKI, XBOOLE_0, PARTFUN1, FUNCT_1, FUNCT_2;
theorem TAMonMon:
::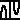
::
[edit]
proof
let A,
B,
C be
set ;
for F being Function of (bool A),(bool B)
for G being Function of (bool B),(bool C)
for H being Function of (bool A),(bool C) st F is anti-monotone & G is monotone & ( for U being Subset of A holds H . U = G . (F . U) ) holds
H is anti-monotone let F be
Function of
(bool A),
(bool B);
for G being Function of (bool B),(bool C)
for H being Function of (bool A),(bool C) st F is anti-monotone & G is monotone & ( for U being Subset of A holds H . U = G . (F . U) ) holds
H is anti-monotone let G be
Function of
(bool B),
(bool C);
for H being Function of (bool A),(bool C) st F is anti-monotone & G is monotone & ( for U being Subset of A holds H . U = G . (F . U) ) holds
H is anti-monotone let H be
Function of
(bool A),
(bool C);
( F is anti-monotone & G is monotone & ( for U being Subset of A holds H . U = G . (F . U) ) implies H is anti-monotone )
assume Z0:
F is
anti-monotone
;
( not G is monotone or ex U being Subset of A st not H . U = G . (F . U) or H is anti-monotone )
assume Z1:
G is
monotone
;
( ex U being Subset of A st not H . U = G . (F . U) or H is anti-monotone )
assume Z2:
for
U being
Subset of
A holds
H . U = G . (F . U)
;
H is anti-monotone
let U be
Subset of
A;
CBS4:def 2 for V being Subset of A st U c= V holds
H . V c= H . Ulet V be
Subset of
A;
( U c= V implies H . V c= H . U )
assume Z3:
U c= V
;
H . V c= H . U
Z4:
F . V c= F . U
by Z3, Z0;
then
G . (F . V) c= G . (F . U)
by Z1;
then
H . V c= G . (F . U)
by Z2;
hence
H . V c= H . U
by Z2;
verum
end;
theorem TMonMon1:
::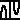
::
[edit]
proof
let A,
B,
C be
set ;
for F being Function of (bool A),(bool B)
for G being Function of (bool B),(bool C) st F is monotone & G is monotone holds
G * F is monotone let F be
Function of
(bool A),
(bool B);
for G being Function of (bool B),(bool C) st F is monotone & G is monotone holds
G * F is monotone let G be
Function of
(bool B),
(bool C);
( F is monotone & G is monotone implies G * F is monotone )
assume Z4:
F is
monotone
;
( not G is monotone or G * F is monotone )
assume Z5:
G is
monotone
;
G * F is monotone
let U be
Subset of
A;
CBS4:def 1 for V being Subset of A st U c= V holds
(G * F) . U c= (G * F) . Vlet V be
Subset of
A;
( U c= V implies (G * F) . U c= (G * F) . V )
assume Z6:
U c= V
;
(G * F) . U c= (G * F) . V
Z7:
(G * F) . U = G . (F . U)
by FUNCT_2:15;
(G * F) . V = G . (F . V)
by FUNCT_2:15;
hence
(G * F) . U c= (G * F) . V
by Z7, Z5, Z6, Z4;
verum
end;
theorem TAMonAMon1:
::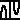
::
[edit]
proof
let A,
B,
C be
set ;
for F being Function of (bool A),(bool B)
for G being Function of (bool B),(bool C) st F is anti-monotone & G is anti-monotone holds
G * F is monotone let F be
Function of
(bool A),
(bool B);
for G being Function of (bool B),(bool C) st F is anti-monotone & G is anti-monotone holds
G * F is monotone let G be
Function of
(bool B),
(bool C);
( F is anti-monotone & G is anti-monotone implies G * F is monotone )
assume Z4:
F is
anti-monotone
;
( not G is anti-monotone or G * F is monotone )
assume Z5:
G is
anti-monotone
;
G * F is monotone
let U be
Subset of
A;
CBS4:def 1 for V being Subset of A st U c= V holds
(G * F) . U c= (G * F) . Vlet V be
Subset of
A;
( U c= V implies (G * F) . U c= (G * F) . V )
assume Z6:
U c= V
;
(G * F) . U c= (G * F) . V
Z7:
(G * F) . U = G . (F . U)
by FUNCT_2:15;
(G * F) . V = G . (F . V)
by FUNCT_2:15;
hence
(G * F) . U c= (G * F) . V
by Z7, Z5, Z6, Z4;
verum
end;
theorem TAMonMon1:
::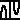
::
[edit]
proof
let A,
B,
C be
set ;
for F being Function of (bool A),(bool B)
for G being Function of (bool B),(bool C) st F is anti-monotone & G is monotone holds
G * F is anti-monotone let F be
Function of
(bool A),
(bool B);
for G being Function of (bool B),(bool C) st F is anti-monotone & G is monotone holds
G * F is anti-monotone let G be
Function of
(bool B),
(bool C);
( F is anti-monotone & G is monotone implies G * F is anti-monotone )
assume Z4:
F is
anti-monotone
;
( not G is monotone or G * F is anti-monotone )
assume Z5:
G is
monotone
;
G * F is anti-monotone
let U be
Subset of
A;
CBS4:def 2 for V being Subset of A st U c= V holds
(G * F) . V c= (G * F) . Ulet V be
Subset of
A;
( U c= V implies (G * F) . V c= (G * F) . U )
assume Z6:
U c= V
;
(G * F) . V c= (G * F) . U
Z7:
(G * F) . U = G . (F . U)
by FUNCT_2:15;
(G * F) . V = G . (F . V)
by FUNCT_2:15;
hence
(G * F) . V c= (G * F) . U
by Z7, Z5, Z6, Z4;
verum
end;
theorem TCBS:
::
::
[edit]
proof
let A,
B be non
empty set ;
for f being Function of A,B
for g being Function of B,A st f is one-to-one & g is one-to-one holds
A,B are_equipotent let f be
Function of
A,
B;
for g being Function of B,A st f is one-to-one & g is one-to-one holds
A,B are_equipotent let g be
Function of
B,
A;
( f is one-to-one & g is one-to-one implies A,B are_equipotent )
assume A0:
(
f is
one-to-one &
g is
one-to-one )
;
A,B are_equipotent
deffunc H1(
Subset of
A)
-> Element of
bool A =
g .: (B \ (f .: (A \ $1)));
consider F being
Function of
(bool A),
(bool A) such that A1:
for
U being
Subset of
A holds
F . U = H1(
U)
from FUNCT_2:sch 4();
A2:
F is
monotone
proof
deffunc H2(
Subset of
A)
-> Element of
bool A =
A \ $1;
deffunc H3(
Subset of
A)
-> Element of
bool B =
f .: $1;
deffunc H4(
Subset of
B)
-> Element of
bool B =
B \ $1;
deffunc H5(
Subset of
B)
-> Element of
bool A =
g .: $1;
consider G1 being
Function of
(bool A),
(bool A) such that B1:
for
U being
Subset of
A holds
G1 . U = H2(
U)
from FUNCT_2:sch 4();
consider G2 being
Function of
(bool A),
(bool B) such that B2:
for
U being
Subset of
A holds
G2 . U = H3(
U)
from FUNCT_2:sch 4();
consider G3 being
Function of
(bool B),
(bool B) such that B3:
for
W being
Subset of
B holds
G3 . W = H4(
W)
from FUNCT_2:sch 4();
consider G4 being
Function of
(bool B),
(bool A) such that B4:
for
W being
Subset of
B holds
G4 . W = H5(
W)
from FUNCT_2:sch 4();
B5:
for
U being
Subset of
A holds
H1(
U)
= H5(
H4(
H3(
H2(
U))))
;
B6:
for
u being
object st
u in bool A holds
(
F . u = G4 . (G3 . (G2 . (G1 . u))) &
F . u = (G4 * (G3 * (G2 * G1))) . u )
then B7:
F = G4 * (G3 * (G2 * G1))
by FUNCT_2:15, FUNCT_2:12;
C1:
G1 is
anti-monotone
by TSetMinusAntimon, B1;
C2:
G2 is
monotone
by TImMon, B2;
C3:
G3 is
anti-monotone
by TSetMinusAntimon, B3;
C4:
G4 is
monotone
by TImMon, B4;
hence
F is
monotone
by B7, C1, C2, C3, C4;
verum
end;
consider C being
Subset of
A such that A3:
F . C = C
by TKnasterTarski, A2;
A4:
C c= A
;
A5:
for
x being
object holds
(
x in C iff
x in g .: (B \ (f .: (A \ C))) )
by A1, A3;
set R =
{ [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } ;
take
{ [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) }
;
TARSKI:def 6 ( ( for b1 being object holds
( not b1 in A or ex b2 being object st
( b2 in B & [b1,b2] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } ) ) ) & ( for b1 being object holds
( not b1 in B or ex b2 being object st
( b2 in A & [b2,b1] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } ) ) ) & ( for b1, b2, b3, b4 being object holds
( not [b1,b2] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or not [b3,b4] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or ( ( not b1 = b3 or b2 = b4 ) & ( not b2 = b4 or b1 = b3 ) ) ) ) )
thus
for
x being
object st
x in A holds
ex
y being
object st
(
y in B &
[x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } )
( ( for b1 being object holds
( not b1 in B or ex b2 being object st
( b2 in A & [b2,b1] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } ) ) ) & ( for b1, b2, b3, b4 being object holds
( not [b1,b2] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or not [b3,b4] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or ( ( not b1 = b3 or b2 = b4 ) & ( not b2 = b4 or b1 = b3 ) ) ) ) )
proof
let x be
object ;
( x in A implies ex y being object st
( y in B & [x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } ) )
assume B0:
x in A
;
ex y being object st
( y in B & [x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } )
reconsider x1 =
x as
Element of
A by B0;
per cases
( not x1 in C or x1 in C )
;
suppose B2:
x1 in C
;
ex y being object st
( y in B & [x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } )
then
x1 in g .: (B \ (f .: (A \ C)))
by A5;
then consider y being
object such that B3:
(
y in B &
y in B \ (f .: (A \ C)) &
x1 = g . y )
by FUNCT_2:64, A5, B2;
take
y
;
( y in B & [x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } )thus
y in B
by B3;
[x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } thus
[x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) }
by B2, B3;
verum
end;
end;
end;
thus
for
y being
object st
y in B holds
ex
x being
object st
(
x in A &
[x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } )
; for b1, b2, b3, b4 being object holds
( not [b1,b2] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or not [b3,b4] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } or ( ( not b1 = b3 or b2 = b4 ) & ( not b2 = b4 or b1 = b3 ) ) )
A6:
for
x,
y being
object st
x in A &
y in B &
x in C &
x = g . y holds
not
y in f .: (A \ C)
;
thus
for
x,
y,
z,
u being
object st
[x,y] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } &
[z,u] in { [x,y] where x is Element of A, y is Element of B : ( ( not x in C & y = f . x ) or ( x in C & x = g . y ) ) } holds
(
x = z iff
y = u )
; verum
end;
:: $\Phi(U)\subseteq \Phi(V)$ forall $U,V\in\wp(A)$ such that $U\subseteq V$.
:: We say $\Phi$ is {\em{antimonotone}} if
:: $\Phi(V)\subseteq \Phi(U)$ forall $U,V\in\wp(A)$ such that $U\subseteq V$.